Construction of Measure
이제 본격적으로 집합을 재보도록 하겠습니다. 우리가 잴 수 있는 집합들부터 시작합니다. \(\mathbb{R}^p\)에서 논의할 건데, 이제 여기서부터는 \(\mathbb{R}\)의 구간의 열림/닫힘을 모두 포괄하여 정의합니다. 즉, \(\mathbb{R}\)의 구간이라고 하면 \([a, b], (a, b), [a, b), (a, b]\) 네 가지 경우를 모두 포함합니다.
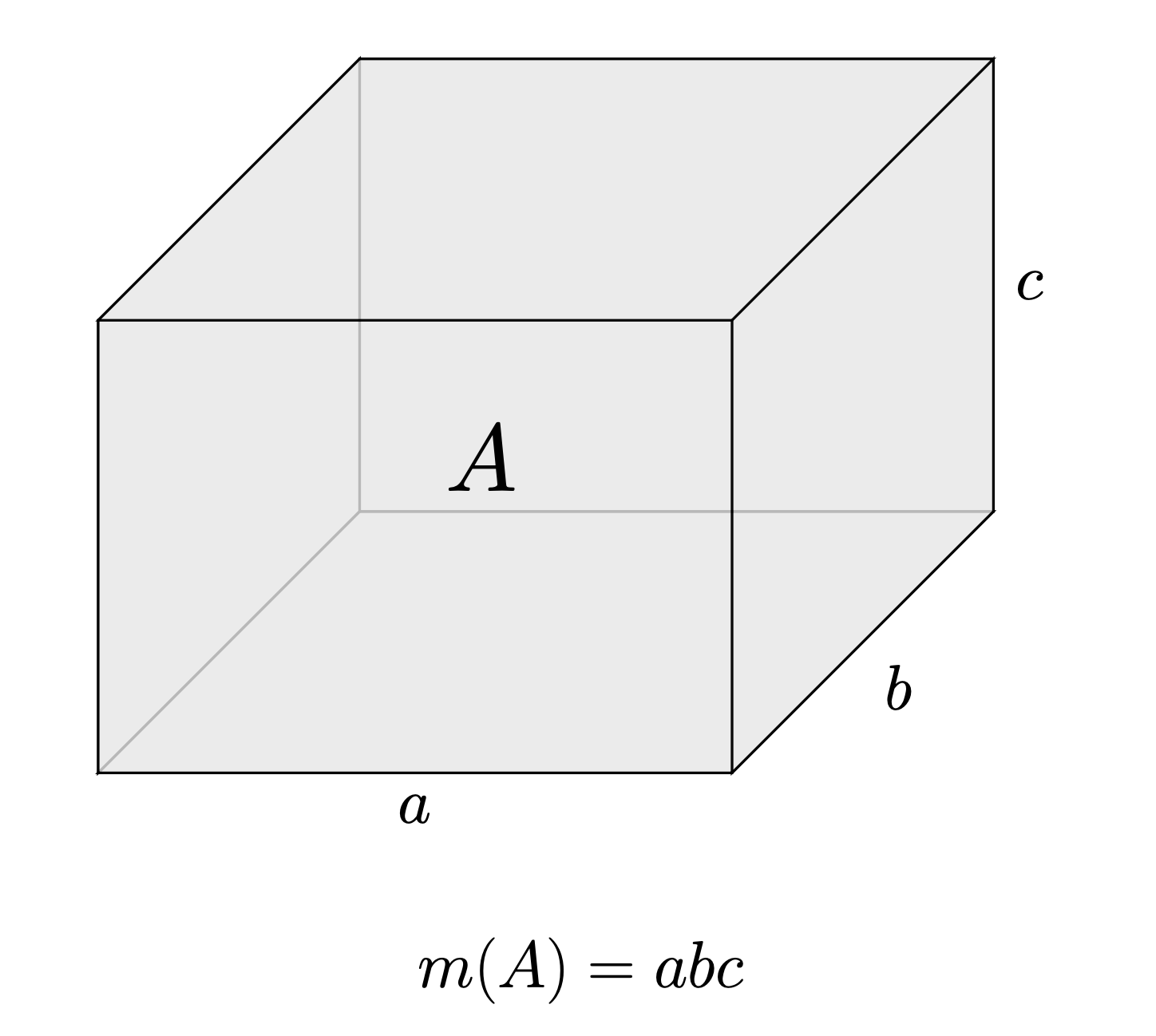
정의. (\(\mathbb{R}^p\)의 구간) \(a_i, b_i \in \mathbb{R}\), \(a_i \leq b_i\) 라 하자. \(I_i\)가 \(\mathbb{R}\)의 구간이라고 할 때, \(\mathbb{R}^p\)의 구간은 \[\prod_{i=1}^p I_i = I_1 \times \cdots \times I_p,\] 와 같이 정의한다.
예를 들어 \(\mathbb{R}^2\)의 구간이라 하면 직사각형 영역, \(\mathbb{R}^3\)의 구간이라 하면 직육면체 영역을 떠올릴 수 있습니다. 단, 경계는 포함되지 않을 수도 있습니다.
이러한 구간들을 유한개 모아 합집합하여 얻은 집합을 모아 elementary set이라 합니다.
정의. (Elementary Set) 어떤 집합이 유한개 구간의 합집합으로 표현되면 그 집합을 elementary set이라고 한다. 그리고 \(\mathbb{R}^p\)의 elementary set의 모임을 \(\Sigma\)로 표기한다.
임의의 구간은 유계입니다. 따라서 구간의 유한한 합집합도 유계일 것입니다.
참고. 임의의 elementary set은 유계이다.
Elementary set의 모임에서 집합의 연산을 정의할 수 있을 것입니다. 이 때, \(\Sigma\)가 ring이 된다는 것을 간단하게 확인할 수 있습니다.
명제. \(\Sigma\)는 ring이다. 하지만 전체 공간인 \(\mathbb{R}^p\)를 포함하고 있지 않기 때문에 \(\sigma\)-ring은 아니다.
구간의 길이를 재는 방법은 아주 잘 알고 있습니다. 유한개 구간의 합집합인 elementary set에서도 쉽게 잴 수 있습니다. 이제 길이 함수 \(m: \Sigma \rightarrow[0, \infty)\) 을 정의하겠습니다. 아직 measure는 아닙니다.
정의. \(a_i, b_i \in \mathbb{R}\) 가 구간 \(I_i\)의 양 끝점이라 하자. \(\mathbb{R}^p\)의 구간 \(I = \displaystyle\prod_{i=1}^p I_i\) 에 대하여, \[m(I) = \prod_{i=1}^p (b_i - a_i)\] 로 정의한다.
정의. \(I_i\)가 쌍마다 서로소인 \(\mathbb{R}^p\)의 구간이라 하자. \(A = \displaystyle\bigcup_{i=1}^n I_i\) 에 대하여 \[m(A) = \sum_{i=1}^n m(I_i)\] 로 정의한다.
\(\mathbb{R}, \mathbb{R}^2, \mathbb{R}^3\)에서 생각해보면 \(m\)은 곧 길이, 넓이, 부피와 대응되는 함수임을 알 수 있습니다. 또한 쌍마다 서로소인 구간의 합집합에 대해서는 각 구간의 함숫값을 더한 것으로 정의합니다. 어떤 집합을 겹치지 않게 구간으로 나눌 수 있다면, 집합의 ‘길이’가 각 구간의 ‘길이’ 합이 되는 것은 자연스럽습니다.
그리고 이 정의는 well-defined 입니다. \(A \in \Sigma\) 에 대해서 서로소인 유한개 구간의 합집합으로 나타내는 방법이 유일하지 않아도, \(m\) 값은 같습니다.
참고. \(m\)은 \(\Sigma\) 위에서 additive이다. 따라서 \(m : \Sigma \rightarrow[0, \infty)\) 은 additive set function이다.
여기서 추가로 regularity 조건을 만족했으면 좋겠습니다.
정의. (Regularity) Set function \(\mu: \Sigma \rightarrow[0, \infty]\) 가 additive라 하자. 모든 \(A \in \Sigma\) 와 \(\epsilon > 0\) 에 대하여
닫힌집합 \(F \in \Sigma\), 열린집합 \(G \in \Sigma\) 가 존재하여 \(F \subseteq A \subseteq G\) 이고 \(\mu(G) - \epsilon \leq \mu(A) \leq \mu(F) + \epsilon\)
이면 \(\mu\)가 \(\Sigma\) 위에서 regular하다고 정의한다.
위에서 정의한 \(m\)이 regular한 것은 쉽게 확인할 수 있습니다.
이제 set function \(\mu: \Sigma \rightarrow[0, \infty)\) 가 finite, regular, additive 하다고 가정합니다.
정의. (Outer Measure) \(E \in \mathcal{P}(\mathbb{R}^p)\) 의 outer measure \(\mu^\ast: \mathcal{P}(\mathbb{R}^p) \rightarrow[0, \infty]\) 는
\(\mu^\ast(E) = \displaystyle \inf \left\{\sum_{n=1}^\infty \mu(A_n) :\right.\) 열린집합 \(A_n \in \Sigma\) 에 대하여 \(\displaystyle\left.E \subseteq\bigcup_{n=1}^\infty A_n\right\}\)
로 정의한다.
Outer measure라 부르는 이유는 \(E\)의 바깥에서 길이를 재서 근사하기 때문입니다. Outer measure는 모든 power set에 대해서 정의할 수 있으니, 이를 이용해서 모든 집합을 잴 수 있으면 좋겠습니다. 하지만 measure가 되려면 countably additive 해야하는데, 이 조건이 가장 만족하기 까다로운 조건입니다. 실제로 countably additive 조건이 성립하지 않습니다.
참고.
- \(\mu^\ast \geq 0\) 이다.
- \(E_1 \subseteq E_2\) 이면 \(\mu^\ast(E_1) \leq \mu^\ast(E_2)\) 이다. (단조성)
정리.
- \(A \in \Sigma\) 이면 \(\mu^\ast(A) = \mu(A)\).1
- Countable subadditivity가 성립한다. \[\mu^\ast\left( \bigcup_{n=1}^\infty E_n \right) \leq \sum_{n=1}^\infty \mu^\ast(E_n), \quad (\forall E_n \in \mathcal{P}(\mathbb{R}^p))\]
증명.
(1) \(A \in \Sigma\), \(\epsilon > 0\) 라 두자. \(\mu\)의 regularity를 이용하면, 열린집합 \(G \in \Sigma\) 가 존재하여 \(A \subseteq G\) 이고 \[\mu^\ast(A) \leq \mu(G) \leq \mu(A) + \epsilon\] 이다. \(\mu^\ast\)의 정의에 의해 열린집합 \(A_n \in \Sigma\) 가 존재하여 \(A \subseteq\displaystyle\bigcup_{n=1}^\infty A_n\) 이고 \[\sum_{n=1}^\infty \mu(A_n) \leq \mu^\ast(A) + \epsilon\] 이다. 마찬가지로 regularity에 의해 닫힌집합 \(F \in \Sigma\) 가 존재하여 \(F\subseteq A\) 이고 \(\mu(A) \leq \mu(F) + \epsilon\) 이다. \(F \subseteq\mathbb{R}^p\) 는 유계이고 닫힌집합이므로 compact set이고, finite open cover를 택할 수 있다.
적당한 \(N \in \mathbb{N}\) 에 대하여 \(F \subseteq\displaystyle\bigcup_{i=1}^N A_{i}\) 가 성립한다.
따라서 \[\mu(A) \leq \mu(F) + \epsilon \leq \sum_{i=1}^N \mu(A_i) \leq \sum_{i=1}^n \mu(A_i) + \epsilon \leq \mu^\ast(A) + 2\epsilon\] 이제 \(\epsilon \rightarrow 0\) 로 두면 \(\mu(A) = \mu^\ast(A)\) 를 얻는다.
(2) 부등식의 양변이 모두 \(\infty\) 이면 증명할 것이 없으므로, 양변이 모두 유한하다고 가정하여 모든 \(n\in \mathbb{N}\) 에 대해 \(\mu^\ast(E_n) < \infty\) 라 하자. \(\epsilon > 0\) 로 두고, 각 \(n \in \mathbb{N}\) 에 대하여 열린집합 \(A_{n, k} \in \Sigma\) 가 존재하여
\(E_n \subseteq\displaystyle\bigcup_{k=1}^\infty A_{n, k}\) 이고 \(\displaystyle\sum_{k=1}^\infty \mu(A_{n,k}) \leq \mu^\ast(E_n) + 2^{-n}\epsilon\)
이다.
\(\mu^\ast\)는 하한(infimum)으로 정의되었기 때문에, \[\mu^\ast\left( \bigcup_{n=1}^\infty E_n \right) \leq \sum_{n=1}^\infty \sum_{k=1}^\infty \mu(A_{n,k}) \leq \sum_{n=1}^\infty \mu^\ast(E_n) + \epsilon\] 가 성립하고, \(\epsilon \rightarrow 0\) 로 두면 부등식이 성립함을 알 수 있다.
Countably additive 조건이 성립하는 집합들만 모아서 measure를 construct 하려고 합니다. 아래 내용은 이를 위한 사전 준비 작업입니다.
표기법. (대칭차집합) \(A \mathop{\mathrm{\triangle}}B = (A\setminus B) \cup (B \setminus A)\).
정의.
- \(d(A, B) = \mu^\ast(A \mathop{\mathrm{\triangle}}B)\) 로 정의한다.
- 집합열 \(A_n\)에 대하여 \(d(A_n, A) \rightarrow 0\) 이면 \(A_n \rightarrow A\) 로 정의한다.
참고.
- \(A, B, C \in \mathbb{R}^p\) 에 대하여 \(d(A, B) \leq d(A, C) + d(C, B)\) 이다.
- \(A_1, B_2, B_1, B_2 \in \mathbb{R}^p\) 일 때, 다음이 성립한다. \[ \left.\begin{array}{c}d(A_1 \cup A_2, B_1 \cup B_2) \\d(A_1 \cap A_2, B_1 \cap B_2) \\d(A_1 \setminus A_2, B_1 \setminus B_2)\end{array}\right\} \leq d(A_1, B_1) + d(A_2, B_2). \]
정의. (Finitely \(\mu\)-measurable) 집합 \(A_n \in \Sigma\) 이 존재하여 \(A_n \rightarrow A\) 이면 \(A\)가 finitely \(\mu\)-measurable이라 한다. 그리고 finitely \(\mu\)-measurable한 집합의 모임을 \(\mathfrak{M}_F(\mu)\)로 표기한다.
위 정의는 \(\mu\)라는 set function에 의해 \(\mu^\ast (A_n \mathop{\mathrm{\triangle}}A) \rightarrow 0\) 이 되는 elementary set \(A_n\)이 존재한다는 의미입니다.
정의. (\(\mu\)-measurable) \(A_n \in \mathfrak{M}_F(\mu)\) 에 대하여 \(A = \displaystyle\bigcup_{n=1}^\infty A_n\) 이면 \(A\)가 \(\mu\)-measurable이라 한다. 그리고 \(\mu\)-measurable한 집합의 모임을 \(\mathfrak{M}(\mu)\)로 표기한다.
참고. \(\mu^\ast(A) = d(A, \varnothing) \leq d(A, B) + \mu^\ast(B)\).
명제. \(\mu^\ast(A)\) 또는 \(\mu^\ast(B)\)가 유한하면, 다음이 성립한다. \[\left| \mu^\ast(A) - \mu^\ast(B) \right| \leq d(A, B).\]
따름정리. \(A \in \mathfrak{M}_F(\mu)\) 이면 \(\mu^\ast(A) < \infty\) 이다.
증명. \(A_n \in \Sigma\) 가 존재하여 \(A_n \rightarrow A\) 이고, \(N \in \mathbb{N}\) 이 존재하여 \[\mu^\ast(A) \leq d(A_N, A) + \mu^\ast(A_N) \leq 1 + \mu^\ast(A_N) < \infty\] 이다.
따름정리. \(A_n \rightarrow A\) 이고 \(A_n, A \in \mathfrak{M}_F(\mu)\) 이면 \(\mu^\ast(A_n)\rightarrow\mu^\ast(A) < \infty\) 이다.
증명. \(\mu^\ast(A)\), \(\mu^\ast(A_n)\)가 유한하므로, \(n \rightarrow\infty\) 일 때 \(\left| \mu^\ast(A_n) - \mu^\ast(A) \right| \leq d(A_n, A) \rightarrow 0\) 이다.
준비가 끝났으니 measure를 construct 해보겠습니다! \(\mathcal{P}(\mathbb{R}^p)\)에서는 할 수 없지만 정의역을 \(\mathfrak{M}(\mu)\)로 조금 좁히면 measure가 된다는 뜻입니다.
정리. \(\mathfrak{M}(\mu)\)는 \(\sigma\)-algebra 이고 \(\mu^\ast\)는 \(\mathfrak{M}(\mu)\)의 measure가 된다.
증명. \(\mathfrak{M}(\mu)\)가 \(\sigma\)-algebra이고 \(\mu^\ast\)가 \(\mathfrak{M}(\mu)\)에서 countably additive임을 보이면 충분하다.
(Step 0) \(\mathfrak{M}_F(\mu)\)는 ring이다.
\(A, B \in \mathfrak{M}_F(\mu)\) 라 하자. 그러면 \(A_n, B_n \in \Sigma\) 이 존재하여 \(A_n \rightarrow A\), \(B_n \rightarrow B\) 이 된다. 그러면 \[ \left.\begin{array}{c}d(A_n \cup B_n, A \cup B) \\ d(A_n \cap B_n, A \cap B) \\ d(A_n \setminus B_n, A \setminus B)\end{array}\right\} \leq d(A_n, A) + d(B_n, B) \rightarrow 0 \] 이므로 \(A_n \cup B_n \rightarrow A \cup B, A_n \setminus B_n \rightarrow A\setminus B\) 이기 때문에 \(\mathfrak{M}_F(\mu)\)는 ring이다.
(Step 1) \(\mu^\ast\)는 \(\mathfrak{M}_F(\mu)\) 위에서 additive이다.
\(\Sigma\) 위에서는 \(\mu = \mu^\ast\) 이므로, 위 따름정리에 의해 \[\begin{matrix} \mu(A_n) \rightarrow\mu^\ast(A), & \mu(A_n\cup B_n) \rightarrow\mu^\ast(A\cup B), \\ \mu(B_n) \rightarrow\mu^\ast(B), & \mu(A_n\cap B_n) \rightarrow\mu^\ast(A\cap B) \end{matrix}\] 가 성립함을 알 수 있다. 일반적으로 \(\mu(A_n) + \mu(B_n) = \mu(A_n \cup B_n) + \mu(A_n \cap B_n)\) 이므로 여기서 \(n \rightarrow\infty\) 로 두면 \[\mu^\ast(A) + \mu^\ast(B) = \mu^\ast(A\cup B) + \mu^\ast(A \cap B)\] 를 얻는다. \(A \cap B = \varnothing\) 라는 조건이 추가되면 \(\mu^\ast\)가 additive임을 알 수 있다.
(Step 2) \(\mathfrak{M}_F(\mu) = \{A \in \mathfrak{M}(\mu) : \mu^\ast(A) < \infty\}\).2
Claim. 쌍마다 서로소인 \(\mathfrak{M}_F(\mu)\)의 원소들을 잡아 이들의 합집합으로 \(A \in \mathfrak{M}(\mu)\) 를 표현할 수 있다.
증명. \(A_n' \in \mathfrak{M}_F(\mu)\) 에 대하여 \(A = \bigcup A_n'\) 로 두자.
\(A_1 = A_1'\), \(n \geq 2\) 이면 \(A_n = A_n' \setminus(A_1'\cup \cdots \cup A_{n-1}')\)
와 같이 정의하면 \(A_n\)이 쌍마다 서로소이고 \(A_n \in \mathfrak{M}_F(\mu)\) 임을 알 수 있다.
위 사실을 이용하여 \(A_n \in \mathfrak{M}_F(\mu)\) 에 대하여 \(A = \displaystyle\bigcup_{n=1}^\infty A_n\) 로 두자.
- Countable subadditivity에 의해 \(\displaystyle\mu^\ast(A) \leq \sum_{n=1}^{\infty} \mu^\ast (A_n)\) 가 성립한다.
- Step 1에 의해 \(\displaystyle\bigcup_{n=1}^k A_n \subseteq A\), \(\displaystyle\sum_{n=1}^{k} \mu^\ast(A_n) \leq \mu^\ast(A)\) 이다. \(k \rightarrow\infty\) 로 두면 \(\displaystyle\mu^\ast(A) \geq \sum_{n=1}^\infty \mu^\ast(A_n)\) 임을 알 수 있다.
따라서 \(\displaystyle\mu^\ast(A) = \sum_{n=1}^\infty \mu^\ast(A_n)\) 이다.3 4
이제 \(B_n =\displaystyle\bigcup_{k=1}^n A_k\) 로 두자. \(\mu^\ast(A) < \infty\) 를 가정하면 \(\displaystyle\sum_{n=1}^\infty \mu^\ast(A_n)\)의 수렴성에 의해
\(\displaystyle d(A, B_n) = \mu^\ast\left( \bigcup_{k=n+1}^\infty A_k \right) = \sum_{k=n+1}^{\infty} \mu^\ast(A_i) \rightarrow 0\) as \(n \rightarrow\infty\)
임을 알 수 있다.
\(B_n \in \mathfrak{M}_F(\mu)\) 이므로 \(C_n \in \Sigma\) 를 잡아 각 \(n \in \mathbb{N}\) 에 대하여 \(d(B_n, C_n)\)를 임의로 작게 만들 수 있다. 그러면 \(d(A, C_n) \leq d(A, B_n) + d(B_n, C_n)\) 이므로 충분히 큰 \(n\)에 대하여 \(d(A, C_n)\)도 임의로 작게 만들 수 있다. 따라서 \(C_n \rightarrow A\) 임을 알 수 있고 \(A \in \mathfrak{M}_F(\mu)\) 라는 결론을 내릴 수 있다.
(Step 3) \(\mu^\ast\)는 \(\mathfrak{M}(\mu)\) 위에서 countably additive이다.
\(A_n \in \mathfrak{M}(\mu)\) 가 \(A \in \mathfrak{M}(\mu)\) 의 분할이라 하자. 적당한 \(m \in \mathbb{N}\) 에 대하여 \(\mu^\ast(A_m) = \infty\) 이면 \[\mu^\ast\left( \bigcup_{n=1}^\infty A_n \right) \geq \mu^\ast(A_m) = \infty = \sum_{n=1}^\infty \mu^\ast(A_n)\] 이므로 countable additivity가 성립한다.
이제 모든 \(n\in \mathbb{N}\) 에 대하여 \(\mu^\ast(A_n) < \infty\) 이면, Step 2에 의해 \(A_n \in \mathfrak{M}_F(\mu)\) 이고 \[\mu^\ast(A) = \mu^\ast\left( \bigcup_{n=1}^\infty A_n \right) = \sum_{n=1}^\infty \mu^\ast(A_n)\] 가 성립한다.
(Step 4) \(\mathfrak{M}(\mu)\)는 \(\sigma\)-ring이다.
\(A_n \in \mathfrak{M}(\mu)\) 이면 \(B_{n, k} \in \mathfrak{M}_F(\mu)\) 가 존재하여 \(\displaystyle A_n = \bigcup_k B_{n,k}\) 이다. 그러면 \[\bigcup_n A_n = \bigcup_{n, k} B_{n, k} \in \mathfrak{M}(\mu)\] 이다.
\(A, B \in \mathfrak{M}(\mu)\) 라 하면 \(A_n, B_n \in \mathfrak{M}_F(\mu)\) 에 대해 \(\displaystyle A = \bigcup A_n\), \(\displaystyle B = \bigcup B_n\) 이므로, \[A \setminus B = \bigcup_{n=1}^\infty \left( A_n \setminus B \right) = \bigcup_{n=1}^\infty (A_n\setminus(A_n\cap B))\] 임을 알 수 있다. 그러므로 \(A_n \cap B \in \mathfrak{M}_F(\mu)\) 인 것만 보이면 충분하다. 정의에 의해 \[A_n \cap B = \bigcup_{k=1}^\infty (A_n \cap B_k) \in \mathfrak{M}(\mu)\] 이고 \(\mu^\ast(A_n \cap B) \leq \mu^\ast(A_n) < \infty\) 이므로 \(A_n\cap B \in \mathfrak{M}_F(\mu)\) 이다. 따라서 \(A \setminus B\) 가 \(\mathfrak{M}_F(\mu)\)의 원소들의 countable 합집합으로 표현되므로 \(A\setminus B \in \mathfrak{M}(\mu)\) 이다.
따라서 \(\mathfrak{M}(\mu)\)는 \(\sigma\)-ring이고 \(\sigma\)-algebra이다.
이제 \(\Sigma\) 위의 \(\mu\) 정의를 \(\mathfrak{M}(\mu)\) (\(\sigma\)-algebra)로 확장하여 \(\mathfrak{M}(\mu)\) 위에서는 \(\mu = \mu^\ast\) 로 정의합니다. \(\Sigma\) 위에서 \(\mu = m\) 일 때, 이와 같이 확장한 \(\mathfrak{M}(m)\) 위의 \(m\)을 Lebesgue measure on \(\mathbb{R}^p\)라 합니다. 그리고 \(A \in \mathfrak{M}(m)\) 를 Lebesgue measurable set이라 합니다.
- \(A\)가 open이 아니면 자명하지 않은 명제입니다.↩︎
- \(A\)가 \(\mu\)-measurable인데 \(\mu^\ast(A) < \infty\)이면 \(A\)는 finitely \(\mu\)-measurable이다.↩︎
- \(A\)가 countable union of sets in \(\mathfrak{M}_F(\mu)\)이므로 \(\mu^\ast\)도 각 set의 \(\mu^\ast\)의 합이 된다.↩︎
- 아직 증명이 끝나지 않았습니다. \(A_n\)은 \(\mathfrak{M}(\mu)\)의 원소가 아니라 \(\mathfrak{M}_F(\mu)\)의 원소입니다.↩︎
'Mathematics > Measure Theory' 카테고리의 다른 글
| 07. Dominated Convergence Theorem (0) | 2023.04.07 |
|---|---|
| 06. Convergence Theorems (0) | 2023.03.25 |
| 05. Lebesgue Integration (0) | 2023.02.13 |
| 04. Measurable Functions (0) | 2023.02.06 |
| 03. Remarks, Measure Spaces (0) | 2023.01.24 |
| 01. Algebra of Sets (0) | 2023.01.11 |



댓글