05. Lebesgue Integration

Lebesgue Integration

르벡 적분을 단계적으로 정의하려고 합니다. $X=(X,\mathcal{F},\mu )$ 라고 계속 가정합니다. $\mathcal{F}$는 $\sigma$-algebra on $X$, $\mu$는 $\mathcal{F}$의 measure 입니다.

$E\in \mathcal{F}$ 일 때, 적분을 정의하기 위해 $${\mathcal{F}}_E=\{A\cap E:A\in \mathcal{F}\},{\mu }_E=\mu {|}_{{\mathcal{F}}_E}$$ 로 설정하고 $\int ={\int }_E$ 로 두어 ($X,{\mathcal{F}}_E,{\mu }_E$) 위에서 적분을 정의할 수 있습니다. 그러나 굳이 이렇게 하지 않아도 됩니다. $\int ={\int }_X$ 로 두고 $${\int }_{E}fd\mu =\int f{\chi }_{E}d\mu$$ 로 정의하면 충분하기 때문입니다. 이제 르벡 적분을 다루기 위해 simple function부터 적분해보겠습니다. 우선 가장 간단한 characteristic function부터 단계를 밟아나가야 합니다.

(Step 1) $A\in \mathcal{F}$ 에 대하여 $$\int {\chi }_{A}d\mu =\mu (A)$$ 로 정의한다.

함수 ${\chi }_A$는 $x\in A$ 일 때만 함숫값 $1$을 갖고 이외의 경우에는 $0$이기 때문에 이 함수를 $X$ 위에서 적분하면 ‘$A$의 길이’에 대응되는 $\mu (A)$가 결과인 것이 자연스럽습니다.

다음으로 양의 값을 갖는 measurable simple function에 대해 정의합니다. $f=f^{+}-f^{-}$ 에서 $f^{+},f^{-}$ 모두 양의 값을 갖기 때문에 양의 값에 대해 먼저 정의합니다.

(Step 2) $f:X\to [0,\mathrm{\infty })$ 가 measurable simple function이라 하자.
그러면 $A_k\subseteq \mathcal{F}$ 이면서 쌍마다 서로소인 집합열 ${\left(A_k\right)}_{k=1}^n$과 $a_k\in [0,\mathrm{\infty })$ 인 수열 ${\left(a_k\right)}_{k=1}^n$을 잡아 $$f(x)=\sum _{k=1}^n{a}_k{\chi }_{A_k}$$ 와 같이 표현할 수 있다. 이제 $$\int fd\mu =\sum _{k=1}^n{a}_k\mu (A_k)\in [0,\mathrm{\infty }]$$ 로 정의한다.

Measurable simple function은 measurable characteristic function의 linear combination으로 표현할 수 있기 때문에, 이와 같은 정의를 생각할 수 있습니다. 하지만 이런 정의를 보면 well-definedness를 제일 먼저 생각해야 합니다. 위와 같은 linear combination 표현이 유일하지 않기 때문입니다.

Well-definedness를 증명하기 위해 임의의 linear combination을 잡아도 적분값이 항상 같음을 보이면 됩니다.

명제. 위 정의는 모든 measurable simple function에 대해 well-defined이다.

증명. $f$가 다음과 같이 두 가지 방법으로 표현된다고 하자. $$f(x)=\sum _{k=1}^n{a}_k{\chi }_{A_k}=\sum _{i=1}^m{b}_i{\chi }_{B_i}.$$ 여기서 $k=1,\dots ,n$, $i=1,\dots ,m$ 에 대하여 $0\le a_k,b_i<\mathrm{\infty }$ 이고 $A_k,B_i\in \mathcal{F}$ 이다. 여기서 $A_k,B_i$는 각각 쌍마다 서로소로, $X$의 분할이 된다. $C_{k,i}=A_k\cap B_i$ 로 두면 $$\sum _{k=1}^n{a}_k\mu (A_k)=\sum _{k=1}^n{a}_k\mu (A_k\cap \bigcup _{i=1}^m{B}_i)=\sum _{k=1}^n\sum _{i=1}^m{a}_k\mu (C_{k,i}),$$ $$\sum _{i=1}^m{b}_i\mu (B_i)=\sum _{i=1}^m{b}_i\mu (B_i\cap \bigcup _{k=1}^n{A}_k)=\sum _{i=1}^m\sum _{k=1}^n{b}_i\mu (C_{k,i})$$ 이다. 이 때 $C_{k,i}\ne \varnothing$ 이면 $x\in C_{k,i}$ 에 대해 $f(x)=a_k=b_i$ 가 된다. 한편 $C_{k,i}=\varnothing$ 이면 $\mu (C_{k,i})=0$ 이다. 이로부터 모든 $k,i$에 대하여 $b_i\mu (C_{k,i})=a_k\mu (C_{k,i})$ 임을 알 수 있다.¹ 따라서 $$\int fd\mu =\sum _{k=1}^n{a}_k\mu (A_k)=\sum _{i=1}^m{b}_i\mu (B_i)$$ 가 되어 적분값은 유일하고 위 정의가 well-defined임을 알 수 있다.

이제 measurable simple function은 얼마든지 적분할 수 있습니다. 이제 다음은 measurable function으로 확장할 단계입니다. 확장을 편하게 하기 위해 약간의 준비 작업을 거치겠습니다.

적분은 선형이고, monotonicity를 항상 유지하기를 기대합니다. 아직은 함수가 $0$보다 클 것을 가정했기 때문에 이를 계속 활용합니다.

참고. $a,b\in [0,\mathrm{\infty })$ 와 measurable simple function $f,g\ge 0$ 에 대하여 $$\int (af+bg)d\mu =a\int fd\mu +b\int gd\mu$$ 이다.

증명. 위 Step 2와 동일하게 $$f=\sum _{j=1}^m{y}_j{\chi }_{A_j},g=\sum _{k=1}^n{z}_k{\chi }_{B_k}$$ 로 둘 수 있다. 여기서 $A_j,B_k$는 $X$의 분할이고 $y_j,z_k\ge 0$ 이다. 마찬가지로 $C_{j,k}=A_j\cap B_k$ 로 정의하면 $$\begin{array}{rl}a\int fd\mu +b\int gd\mu & =\sum _{j}a{y}_j\mu (A_j)+\sum _{k}b{z}_k\mu (B_k)\\ & =\sum _{j}a{y}_j\sum _k\mu (A_j\cap B_k)+\sum _{k}b{z}_k\sum _j\mu (B_k\cap A_j)\\ & =\sum _j\sum _{k}a{y}_j\mu (C_{j,k})+\sum _k\sum _{j}b{z}_k\mu (C_{j,k})\\ & =\sum _{j,k}(a{y}_j+b{z}_k)\mu (C_{j,k})=\int (af+bg)d\mu \end{array}$$ 이다.

참고. $f\ge g\ge 0$ 이 measurable simple function일 때, $$\int fd\mu \ge \int gd\mu$$ 이다.

증명. $f-g\ge 0$ 이 simple이고 measurable임을 활용한다. $$\int fd\mu =\int [g+(f-g)]d\mu =\int gd\mu +\int (f-g)d\mu \ge \int gd\mu \ge 0.$$

위와 같이 $g+(f-g)$ 로 변형해야 하는 이유는 $g$의 적분값이 무한대인 경우 이를 이항할 수 없기 때문입니다. 하지만 $f-g$ 의 적분값이 $0$ 이상인 것은 확실하게 알 수 있습니다.

이제 양의 값을 가지는 임의의 measurable function을 고려해 보겠습니다.

(Step 3) $f:X\to [0,\mathrm{\infty }]$ 가 measurable일 때, $$\int fd\mu =sup\{\int hd\mu :0\le h\le f,h\text{ measurable and simple}\}.$$ 로 정의한다.

$f$보다 작은 measurable simple function의 적분값 중 상한을 택하겠다는 의미입니다. $f$보다 작은 measurable simple function으로 $f$를 근사한다고도 이해할 수 있습니다. 또한 $f$가 simple function이면 Step 2의 정의와 일치하는 것을 알 수 있습니다.

$f\ge 0$ 가 measurable이면 증가하는 measurable simple 함수열 $s_n$이 존재함을 지난 번에 보였습니다. 이 $s_n$에 대하여 적분값을 계산해보면 $${\int }_E{s}_{n}d\mu =\sum _{i=1}^{n{2}^n}\frac{i-1}{2^n}\mu \left(\{x\in E:\frac{i-1}{2^n}\le f(x)\le \frac{i}{2^n}\}\right)+n\mu (\{x\in E:f(x)\ge n\})$$ 임을 알 수 있습니다. 이제 $n\to \mathrm{\infty }$ 일 때 우변이 곧 ${\displaystyle \int fd\mu }$ 이기를 기대합니다.

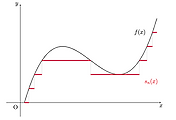
위 내용에 대한 증명은 추후 다루도록 하고 식의 의미를 이해해 보겠습니다. 르벡 적분은 치역을 잘게 잘라 자른 치역 부분의 preimage에 대해 measure를 사용하여 길이를 잽니다. 그리고 함숫값과 preimage의 measure를 곱한 뒤 더해 넓이를 계산한다고 이해할 수 있습니다. 리만 적분은 정의역을 잘게 잘라 상합/하합을 고려하여 정의한 것과는 다른 접근 방법입니다.

이제 마지막 단계입니다. 임의의 measurable function에 대해 정의합니다.

(Step 4) $f$가 measurable이면 $f^{+},f^{-}\ge 0$ 도 measurable이다. 그러므로 $E\in \mathcal{F}$ 에 대하여 $${\int }_{E}fd\mu ={\int }_E{f}^{+}d\mu -{\int }_E{f}^{-}d\mu$$ 와 같이 정의한다. 단, 우변에서 $\mathrm{\infty }-\mathrm{\infty }$ 가 등장하는 경우는 제외한다.

우변에서 $\mathrm{\infty }-\mathrm{\infty }$ 인 경우는 제외되었기 때문에 $f^{+}$, $f^{-}$의 적분값 둘 중 하나는 유한해야 합니다.

위 내용을 종합하여 다음 정의를 얻습니다.

정의. (르벡 적분 가능) $f$가 measurable이고, $${\int }_E\left|f\right|d\mu ={\int }_E{f}^{+}d\mu +{\int }_E{f}^{-}d\mu <\mathrm{\infty }$$ 이면 $f$가 $E$에서 $\mu$에 대해 르벡 적분 가능하다고 한다.

표기법. $f$가 $E$에서 $\mu$에 대해 르벡 적분 가능하면 $$f\in {\mathcal{L}}^1(E,\mu )$$ 로 표기한다. 특별히 $\mu =m$ 이면 $f\in {\mathcal{L}}^1(E)$ 로 적는다.

즉 다음이 성립합니다. $$f\in {\mathcal{L}}^1(E,\mu )⟺f^{+},f^{-}\in {\mathcal{L}}^1(E,\mu )⟺\left|f\right|\in {\mathcal{L}}^1(E,\mu ).$$

---

다음 글에서는 르벡 적분의 성질과 수렴 정리에 대해 다루도록 하겠습니다.

---

1. 계수가 같거나, measure가 0이 되어 같거나.↩︎