 08. Comparison with the Riemann Integral
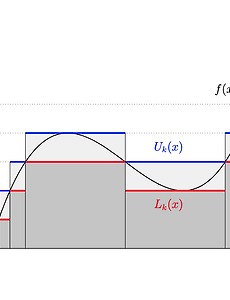
Comparison with the Riemann Integral 먼저 혼동을 막기 위해 Lebesgue measure \(m\)에 대하여 르벡 적분을 \[\int_{[a, b]} f \,d{m} = \int_{[a, b]} f \,d{x} = \int_a^b f \,d{x}\] 와 같이 표기하고, 리만 적분은 \[\mathcal{R}\int_a^b f\,d{x}\] 로 표기하겠습니다. 정리. \(a, b \in \mathbb{R}\) 에 대하여 \(a < b\) 이고 함수 \(f\)가 유계라고 하자. \(f \in \mathcal{R}[a, b]\) 이면 \(f \in \mathcal{L}^{1}[a, b]\) 이고 \(\displaystyle\int_a^b f\,d{x} = \mathcal{R}\in..
2023. 6. 20.
08. Comparison with the Riemann Integral
Comparison with the Riemann Integral 먼저 혼동을 막기 위해 Lebesgue measure \(m\)에 대하여 르벡 적분을 \[\int_{[a, b]} f \,d{m} = \int_{[a, b]} f \,d{x} = \int_a^b f \,d{x}\] 와 같이 표기하고, 리만 적분은 \[\mathcal{R}\int_a^b f\,d{x}\] 로 표기하겠습니다. 정리. \(a, b \in \mathbb{R}\) 에 대하여 \(a < b\) 이고 함수 \(f\)가 유계라고 하자. \(f \in \mathcal{R}[a, b]\) 이면 \(f \in \mathcal{L}^{1}[a, b]\) 이고 \(\displaystyle\int_a^b f\,d{x} = \mathcal{R}\in..
2023. 6. 20.
 02. Construction of Measure
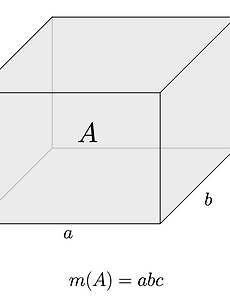
Construction of Measure 이제 본격적으로 집합을 재보도록 하겠습니다. 우리가 잴 수 있는 집합들부터 시작합니다. \(\mathbb{R}^p\)에서 논의할 건데, 이제 여기서부터는 \(\mathbb{R}\)의 구간의 열림/닫힘을 모두 포괄하여 정의합니다. 즉, \(\mathbb{R}\)의 구간이라고 하면 \([a, b], (a, b), [a, b), (a, b]\) 네 가지 경우를 모두 포함합니다. 정의. (\(\mathbb{R}^p\)의 구간) \(a_i, b_i \in \mathbb{R}\), \(a_i \leq b_i\) 라 하자. \(I_i\)가 \(\mathbb{R}\)의 구간이라고 할 때, \(\mathbb{R}^p\)의 구간은 \[\prod_{i=1}^p I_i = I_1 \..
2023. 1. 23.
02. Construction of Measure
Construction of Measure 이제 본격적으로 집합을 재보도록 하겠습니다. 우리가 잴 수 있는 집합들부터 시작합니다. \(\mathbb{R}^p\)에서 논의할 건데, 이제 여기서부터는 \(\mathbb{R}\)의 구간의 열림/닫힘을 모두 포괄하여 정의합니다. 즉, \(\mathbb{R}\)의 구간이라고 하면 \([a, b], (a, b), [a, b), (a, b]\) 네 가지 경우를 모두 포함합니다. 정의. (\(\mathbb{R}^p\)의 구간) \(a_i, b_i \in \mathbb{R}\), \(a_i \leq b_i\) 라 하자. \(I_i\)가 \(\mathbb{R}\)의 구간이라고 할 때, \(\mathbb{R}^p\)의 구간은 \[\prod_{i=1}^p I_i = I_1 \..
2023. 1. 23.