06. Convergence Theorems

Convergence Theorems

르벡 적분 이론에서 굉장히 자주 사용되는 수렴 정리에 대해 다루겠습니다. 이 정리들을 사용하면 굉장히 유용한 결과를 쉽게 얻을 수 있습니다.

먼저 단조 수렴 정리(monotone convergence theorem, MCT)입니다. 이 정리에서는 $f_n\ge 0$ 인 것이 매우 중요합니다.

정리. (단조 수렴 정리) $f_n:X\to [0,\mathrm{\infty }]$ 가 measurable이고 모든 $x\in X$ 에 대하여 $f_n(x)\le f_{n+1}(x)$ 라 하자. $$\underset{n\to \mathrm{\infty }}{lim}{f}_n(x)=\underset{n}{sup}{f}_n(x)=f(x)$$ 로 두면, $$\int fd\mu =\underset{n\to \mathrm{\infty }}{lim}\int f_{n}d\mu =\underset{n\in \mathbb{N}}{sup}\int f_{n}d\mu$$ 이다.

증명.
($\ge$) $f_n(x)\le f(x)$ 이므로 단조성을 이용하면 모든 $n\in \mathbb{N}$ 에 대하여 ${\displaystyle \int f_{n}d\mu \le {\displaystyle \int fd\mu }}$ 이다. 따라서 다음이 성립한다. $$\underset{n}{sup}\int f_{n}d\mu \le \int fd\mu .$$

($\le$) 실수 $c\in (0,1)$ 를 잡자. 마지막에 $c\nearrow 1$ 로 둘 것이다. 이제 measurable simple function $s$가 $0\le s\le f$ 라 하자. 그러면 모든 $x\in X$ 에 대하여 $c\cdot s(x)<f(x)$ 일 것이다.

이제 $$E_n=\{x\in X:f_n(x)\ge cs(x)\}$$ 으로 두면, $f_n(x)-cs(x)$ 가 measurable function이므로 $E_n$ 또한 measurable이다. 여기서 $f_n$이 증가하므로 $E_n\subseteq E_{n+1}\subseteq \cdots$ 임을 알 수 있고 $f_n\to f$ 이므로 $\bigcup _{n=1}^{\mathrm{\infty }}{E}_n=X$ 이다.

충분히 큰 $N\in \mathbb{N}$ 에 대하여 $n\ge N$ 일 때, 모든 $x$에 대하여 $f(x)\ge f_n(x)>cs(x)$ 가 되게 할 수 있다. 그리고 $f_n\ge f_n{\chi }_{E_n}\ge cs{\chi }_{E_n}$ 이므로 $$\begin{array}{}\text{(}\star \text{)}& \int f_{n}d\mu \ge \int f_n{\chi }_{E_n}d\mu \ge c\int s{\chi }_{E_n}d\mu ,\end{array}$$ 이고 여기서 $s,{\chi }_{E_n}$는 simple function이다. 그러므로 $s=\sum _{k=0}^m{y}_k{\chi }_{A_k}$ 라고 적으면 $$s{\chi }_{E_n}=\sum _{k=0}^m{y}_k{\chi }_{A_k\cap E_n}⟹\int s{\chi }_{E_n}d\mu =\sum _{k=0}^m{y}_k\mu (A_k\cap E_n)$$ 이다. $n\to \mathrm{\infty }$ 일 때 $A_k\cap E_n\nearrow A_k$ 이므로, continuity of measure를 사용해 $\mu (A_k\cap E_n)\nearrow \mu (A_k)$ 를 얻고 $$\underset{n\to \mathrm{\infty }}{lim}\int s{\chi }_{E_n}d\mu =\int sd\mu$$ 임도 알 수 있다. 이제 ($\star$)를 이용하면 $$\underset{n\to \mathrm{\infty }}{lim}\int f_{n}d\mu \ge c\int sd\mu$$ 이므로, $c\nearrow 1$ 로 두고 $0\le s\le f$ 에 대하여 $sup$을 취하면 $$\underset{n\to \mathrm{\infty }}{lim}\int f_{n}d\mu \ge \underset{0\le s\le f}{sup}\int sd\mu =\int fd\mu$$ 가 되어 원하는 결과를 얻는다.

참고. 만약 부등식 $0\le f_n\le f_{n+1}$ 이 정의역 전체가 아닌 정의역의 부분집합 $E$에서만 성립한다고 하면, 다음과 같이 생각할 수 있다. $$0\le f_n{\chi }_E\le f_{n+1}{\chi }_E\nearrow f{\chi }_E.$$ 그러므로 단조 수렴 정리가 $E$에서도 성립함을 알 수 있다.

$E$에서 $0\le f_n\le f_{n+1}\nearrow f$ 이면 ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}{\int }_E{f}_{n}d\mu ={\int }_{E}fd\mu }$.

참고. 함수열 $f_n$이 증가하는 경우에만 정리가 성립합니다. 감소하는 경우에는 반례로 함수 $f_n={\chi }_{[n,\mathrm{\infty })}$ 를 생각할 수 있습니다. 그러면 $n\to \mathrm{\infty }$ 일 때 ${\chi }_{[n,\mathrm{\infty })}\searrow 0$ 입니다.

그러면 Lebesgue measure $m$에 대하여 $$\mathrm{\infty }=\int {\chi }_{[n,\mathrm{\infty })}dm\ne \int 0dm=0$$ 이 되어 단조 수렴 정리가 성립하지 않음을 확인할 수 있습니다.

---

지난 번에 $f\ge 0$ 가 measurable이면 증가하는 measurable simple 함수열 $s_n$이 존재함을 보였고, 이 $s_n$에 대하여 적분값을 계산하여 $${\int }_E{s}_{n}d\mu =\sum _{i=1}^{n{2}^n}\frac{i-1}{2^n}\mu \left(\{x\in E:\frac{i-1}{2^n}\le f(x)\le \frac{i}{2^n}\}\right)+n\mu (\{x\in E:f(x)\ge n\})$$ 라는 결과까지 얻었습니다. 그런데 여기서 $$f(x)={\displaystyle \underset{n\to \mathrm{\infty }}{lim}{s}_n(x)}$$ 이기 때문에, 단조 수렴 정리에 의해 $${\int }_{E}fd\mu =\underset{n\to \mathrm{\infty }}{lim}{\int }_E{s}_{n}d\mu$$ 가 성립하여 기대했던 결과를 얻었습니다. 지난 번 설명한 것처럼, 이는 곧 르벡 적분은 치역을 잘게 잘라 넓이를 계산한 것으로 이해할 수 있다는 의미가 됩니다.

다음은 단조 수렴 정리를 활용하여 유용한 결과를 쉽게 얻을 수 있는 예제입니다.

참고. Measurable function $f,g\ge 0$ 과 $\alpha ,\beta \in [0,\mathrm{\infty })$ 에 대하여 다음이 성립한다. $${\int }_E(\alpha f+\beta g)d\mu =\alpha {\int }_{E}fd\mu +\beta {\int }_{E}gd\mu .$$

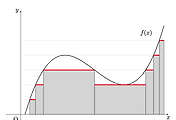
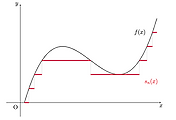
증명. Measurable function은 measurable simple function으로 근사할 수 있고, $f,g\ge 0$ 이므로 단조증가하도록 잡을 수 있다. 그러므로 measurable simple function $f_n$, $g_n$에 대하여 $0\le f_n\le f_{n+1}\nearrow f$, $0\le g_n\le g_{n+1}\nearrow g$ 으로 잡는다.

그러면 $\alpha f_n+\beta g_n\nearrow \alpha f+\beta g$ 이고 $\alpha f_n+\beta g_n$ 은 단조증가하는 measurable simple 함수열이다. 따라서 단조 수렴 정리에 의해 $${\int }_E(\alpha f_n+\beta g_n)d\mu =\alpha {\int }_E{f}_{n}d\mu +\beta {\int }_E{g}_{n}d\mu \to \alpha {\int }_{E}fd\mu +\beta {\int }_{E}gd\mu$$ 이다.

이와 비슷한 방법을 급수에도 적용할 수 있습니다.

정리. Measurable function $f_n:X\to [0,\mathrm{\infty }]$ 에 대하여 $\sum _{n=1}^{\mathrm{\infty }}{f}_n$는 measurable이고, 단조 수렴 정리에 의해 다음이 성립한다. $${\int }_E\sum _{n=1}^{\mathrm{\infty }}{f}_{n}d\mu =\sum _{n=1}^{\mathrm{\infty }}{\int }_E{f}_{n}d\mu .$$

증명. $\sum _{n=1}^{\mathrm{\infty }}{f}_n$는 measurable function의 극한이므로 measurable이다. 무한급수를 부분합의 극한으로 생각하면 $f_n\ge 0$ 이므로 부분합이 증가함을 알 수 있다. 따라서 단조 수렴 정리를 적용하여 결론을 얻는다.

---

단조 수렴 정리와 동치인 수렴 정리를 하나 더 소개합니다. Fatou lemma로 알려져 있습니다.

정리. (Fatou) $f_n\ge 0$ 가 measurable이고 $E$가 measurable이라 하자. 다음이 성립한다. $${\int }_E\underset{n\to \mathrm{\infty }}{lim inf}{f}_{n}d\mu \le \underset{n\to \mathrm{\infty }}{lim inf}{\int }_E{f}_{n}d\mu .$$

증명. $g_n={\displaystyle \underset{k\ge n}{inf}{f}_k}$ 으로 두면 ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}{g}_n=\underset{n\to \mathrm{\infty }}{lim inf}{f}_n}$ 이다. $g_n$이 증가함은 쉽게 확인할 수 있으며 $g_n\ge 0$ 이다. $g_n$의 정의로부터 모든 $k\ge n$ 에 대하여 $g_n\le f_k$ 이므로, $${\int }_E{g}_{n}d\mu \le \underset{k\ge n}{inf}{\int }_E{f}_{k}d\mu$$ 이다. 여기서 $n\to \mathrm{\infty }$ 로 두면 $${\int }_E\underset{n\to \mathrm{\infty }}{lim inf}{f}_{n}d\mu =\underset{n\to \mathrm{\infty }}{lim}{\int }_E{g}_{n}d\mu \le \underset{n\to \mathrm{\infty }}{lim}\underset{k\ge n}{inf}{\int }_E{f}_{k}d\mu =\underset{n\to \mathrm{\infty }}{lim inf}{\int }_E{f}_{n}d\mu$$ 이 된다. 여기서 첫 번째 등호는 단조 수렴 정리에 의해 성립한다.

참고. 위 증명에서는 단조 수렴 정리를 활용했습니다. 반대로 이 정리를 가정하면 단조 수렴 정리를 증명할 수 있기도 합니다. 따라서 이 둘은 동치입니다. 증명은 생략합니다.

참고. 왠지 위와 비슷한 결론이 $lim sup$에 대해서도 성립해야 할 것 같습니다. 구체적으로, $${\int }_E\underset{n\to \mathrm{\infty }}{lim sup}{f}_{n}d\mu \ge \underset{n\to \mathrm{\infty }}{lim sup}{\int }_E{f}_{n}d\mu$$ 일 것 같습니다. 안타깝게도 이는 성립하지 않습니다. 반례로 앞서 소개한 ${\chi }_{[n,\mathrm{\infty })}$를 한 번 더 가져올 수 있습니다. 좌변을 계산해 보면 0이지만, 우변을 계산해 보면 $\mathrm{\infty }$입니다. 나중에 소개하겠지만, $\left|f_n\right|\le g$ 를 만족하는 함수 $g\in {\mathcal{L}}^1$ 가 존재해야 위 부등식이 성립합니다.

참고. 르벡 적분의 몇 가지 성질을 소개하고 마칩니다.

1. $f$가 measurable이고 $E$에서 bounded이며 $\mu (E)<\mathrm{\infty }$ 일 때, 적당한 실수 $M>0$ 에 대하여 $\left|f\right|\le M$ 이므로 $${\int }_E\left|f\right|d\mu \le {\int }_{E}Md\mu =M\mu (E)<\mathrm{\infty }$$ 임을 알 수 있습니다. 그러므로 $f\in {\mathcal{L}}^1(E,\mu )$ 입니다. $E$의 measure가 finite라는 가정 하에, bounded function은 모두 르벡 적분 가능합니다.
2. $f,g\in {\mathcal{L}}^1(E,\mu )$ 이고 $E$에서 $f\le g$ 일 때, 단조성이 성립함을 보이려고 합니다. 앞에서는 $0\le f\le g$ 인 경우에만 단조성을 증명했었는데, 이를 확장하여 함수가 음의 값을 가지는 경우에도 증명하고 싶습니다. 그러므로 양수인 부분과 음수인 부분을 나누어 고려하여 다음과 같이 적을 수 있습니다. $${\chi }_E(x)f^{+}(x)\le {\chi }_E(x)g^{+}(x),{\chi }_E(x)g^{-}(x)\le {\chi }_E(x)f^{-}(x)$$ 이로부터 $${\int }_E{f}^{+}d\mu \le {\int }_E{g}^{+}d\mu <\mathrm{\infty },{\int }_E{g}^{-}d\mu \le {\int }_E{f}^{-}d\mu <\mathrm{\infty }$$ 를 얻습니다. 따라서 $${\int }_{E}fd\mu \le {\int }_{E}gd\mu$$ 가 성립하고, 함수가 음의 값을 가지는 경우에도 단조성이 성립함을 알 수 있습니다.
3. $f\in {\mathcal{L}}^1(E,\mu )$, $c\in \mathbb{R}$ 라 하면 $cf\in {\mathcal{L}}^1(E,\mu )$ 입니다. 왜냐하면 $${\int }_E\left|c\right|\left|f\right|d\mu =\left|c\right|{\int }_E\left|f\right|d\mu <\mathrm{\infty }$$ 이기 때문입니다. 적분이 가능하니 실제 적분값을 계산할 때 선형성이 성립했으면 좋겠습니다. 앞에서는 음이 아닌 실수에 대해서만 증명했었는데, 이도 마찬가지로 확장하려 합니다. $c<0$ 인 경우만 보이면 됩니다. 이 때, $(cf{)}^{+}=-c{f}^{-}$, $(cf{)}^{-}=-c{f}^{+}$ 이므로, 다음이 성립합니다. $${\int }_{E}cfd\mu ={\int }_E(cf{)}^{+}-{\int }_E(cf{)}^{-}d\mu =-c{\int }_E{f}^{-}d\mu -(-c){\int }_E{f}^{+}d\mu =c{\int }_{E}fd\mu .$$
4. Measurable function $f$에 대하여 $E$에서 $a\le f(x)\le b$ 이고 $\mu (E)<\mathrm{\infty }$ 일 때 다음이 성립합니다. $${\int }_{E}a{\chi }_{E}d\mu \le {\int }_{E}f{\chi }_{E}d\mu \le {\int }_{E}b{\chi }_{E}d\mu ⟹a\mu (E)\le {\int }_{E}fd\mu \le b\mu (E).$$ $f$가 르벡 적분 가능하다는 사실은 $f$가 bounded라는 사실을 이용합니다.
5. $f\in {\mathcal{L}}^1(E,\mu )$ 와 measurable set $A\subseteq E$ 가 주어지는 경우, $f$는 $E$의 부분집합인 $A$ 위에서도 르벡 적분 가능합니다. 이는 다음 부등식에서 확인할 수 있습니다. $${\int }_A\left|f\right|d\mu \le {\int }_E\left|f\right|d\mu <\mathrm{\infty }.$$
6. 만약 measure가 0인 집합에서 적분을 하면 어떻게 될까요? $\mu (E)=0$ 라 하고, measurable function $f$를 적분해 보겠습니다. 여기서 $min\{\left|f\right|,n\}{\chi }_E$ 도 measurable이며 $n\to \mathrm{\infty }$ 일 때 $min\{\left|f\right|,n\}{\chi }_E\nearrow \left|f\right|{\chi }_E$ 임을 이용합니다. 마지막으로 단조 수렴 정리를 적용하면 $$\begin{array}{rl}{\int }_E\left|f\right|d\mu & =\underset{n\to \mathrm{\infty }}{lim}{\int }_{E}min\{\left|f\right|,n\}d\mu \\ & \le \underset{n\to \mathrm{\infty }}{lim}{\int }_{E}nd\mu =\underset{n\to \mathrm{\infty }}{lim}n\mu (E)=0\end{array}$$ 임을 얻습니다. 따라서 $f\in {\mathcal{L}}^1(E,\mu )$ 이고, ${\displaystyle {\int }_{E}fd\mu =0}$ 가 되어 적분값이 0임을 알 수 있습니다. 즉, measure가 0인 집합 위에서 적분하면 그 결과는 0이 됩니다.¹

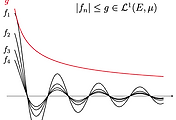
다음 글에서는 르벡 수렴 정리를 소개하겠습니다.

---

1. 편의상 $0\cdot \mathrm{\infty }=0$ 으로 정의했기 때문에 $f\equiv \mathrm{\infty }$ 인 경우에도 성립합니다.↩︎