08. Comparison with the Riemann Integral

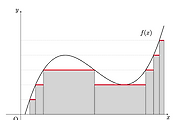
Comparison with the Riemann Integral

먼저 혼동을 막기 위해 Lebesgue measure \(m\)에 대하여 르벡 적분을 \[\int_{[a, b]} f \,d{m} = \int_{[a, b]} f \,d{x} = \int_a^b f \,d{x}\] 와 같이 표기하고, 리만 적분은 \[\mathcal{R}\int_a^b f\,d{x}\] 로 표기하겠습니다.

정리. \(a, b \in \mathbb{R}\) 에 대하여 \(a < b\) 이고 함수 \(f\)가 유계라고 하자.

1. \(f \in \mathcal{R}[a, b]\) 이면 \(f \in \mathcal{L}^{1}[a, b]\) 이고 \(\displaystyle\int_a^b f\,d{x} = \mathcal{R}\int_a^b f \,d{x}\) 이다.
2. \(f \in \mathcal{R}[a, b]\) \(\iff\) \(f\)가 연속 \(m\)-a.e. on \([a, b]\).

쉽게 풀어서 적어보면, (1)은 \(f\)가 \([a, b]\)에서 리만 적분 가능하면 르벡 적분 또한 가능하며, 적분 값이 같다는 의미입니다. 즉 르벡 적분이 리만 적분보다 더 강력하다는 것을 알 수 있습니다.

또한 (2)는 리만 적분 가능성에 대한 동치 조건을 알려줍니다. Almost everywhere라는 조건이 붙었기 때문에, \(\mathcal{L}^1\)의 equivalence class를 고려하면 사실상 연속함수에 대해서만 리만 적분이 가능하다는 뜻이 됩니다.

증명. \(k \in \mathbb{N}\) 에 대하여 구간 \([a, b]\)의 분할 \(P_k = \{a = x_0^k < x_1^k < \cdots < x_{n_k}^k = b\}\) 를 잡는다. 단 \(P_k \subseteq P_{k+1}\) (refinement) 이고 \(\left| x_{i}^k - x_{i-1}^k \right| < \frac{1}{k}\) 이 되도록 한다.

그러면 리만 적분의 정의로부터 \[\lim_{k \rightarrow\infty} L(P_k, f) = \mathcal{R}\underline{\int_{a}^{b}} f\,d{x}, \quad \lim_{k \rightarrow\infty} U(P_k, f) = \mathcal{R} \overline{\int_{a}^{b}} f \,d{x}\] 임을 알 수 있다.

이제 measurable simple function \(U_k, L_k\)를 다음과 같이 잡는다. \[U_k = \sum_{i=1}^{n_k} \sup_{x_{i-1}^k \leq y \leq x_{i}^k} f(y) \chi_{(x_{i-1}^k, x_i^k]}, \quad L_k = \sum_{i=1}^{n_k} \inf_{x_{i-1}^k \leq y \leq x_{i}^k} f(y) \chi_{(x_{i-1}^k, x_i^k]}.\] 그러면 구간 \([a, b]\) 위에서 \(L_k \leq f \leq U_k\)인 것은 당연하고, 르벡 적분이 가능하므로 \[\int_a^b L_k \,d{x} = L(P_k, f), \quad \int_a^b U_k \,d{x} = U(P_k, f)\] 이 됨을 알 수 있다. 여기서 \(P_k \subseteq P_{k + 1}\) 이 되도록 잡았기 때문에, \(L_k\)는 증가하는 수열, \(U_k\)는 감소하는 수열이다.

그러므로 \[L(x) = \lim_{k \rightarrow\infty} L_k(x), \quad U(x) = \lim_{k \rightarrow\infty} U_k(x)\] 로 정의했을 때, 극한이 존재함을 알 수 있다. 여기서 \(f, L_k, U_k\)가 모두 유계인 함수이므로 지배 수렴 정리에 의해 \[\int_a^b L \,d{x} = \lim_{k \rightarrow\infty} \int_a^b L_k \,d{x} = \lim_{k \rightarrow\infty} L(P_k, f) = \mathcal{R}\underline{\int_{a}^{b}} f\,d{x} < \infty,\] \[\int_a^b U\,d{x} = \lim_{k \rightarrow\infty} \int_a^b U_k \,d{x} = \lim_{k \rightarrow\infty} U(P_k, f) = \mathcal{R} \overline{\int_{a}^{b}} f \,d{x} < \infty\] 이므로 \(L, U \in \mathcal{L}^{1}[a, b]\) 이다.

위 사실을 종합하면 \(f \in \mathcal{R}[a, b]\) 일 때, \[\mathcal{R}\underline{\int_{a}^{b}} f\,d{x} = \mathcal{R}\overline{\int_{a}^{b}} f\,d{x}\] 이므로 \[\int_a^b (U - L)\,d{x} = 0\] 가 되어 \(U = L\) \(m\)-a.e. on \([a, b]\)라는 사실을 알 수 있다. 역으로 이를 거꾸로 읽어보면 \(U = L\) \(m\)-a.e. on \([a, b]\)일 때 \(f \in \mathcal{R}[a, b]\) 가 되는 것 또한 알 수 있다.

(1) 위 논의에 의해 \(f \in \mathcal{R}[a, b]\) 이면 \(f = U = L\) a.e. on \([a, b]\) 이다. 따라서 \(f\)는 measurable. \[\int_a^b f \,d{x} = \mathcal{R}\int_a^b f\,d{x} < \infty \implies f \in \mathcal{L}^{1}[a, b].\]

(2) 만약 \(x \notin \bigcup_{k=1}^{\infty} P_k\) 라고 가정하면, 임의의 \(\epsilon > 0\) 에 대해 충분히 큰 \(n \in \mathbb{N}\) 을 잡았을 때 적당한 \(j_0 \in \mathbb{N}\) 이 존재하여 \(x \in (t_{j_0-1}^n, t_{j_0}^n)\) 이면서 \[\left| L_n(x) - L(x) \right| + \left| U_n(x) - U(x) \right| < \epsilon\] 이 되도록 할 수 있다. 그러면 \(y \in (t_{j_0-1}^n, t_{j_0}^n)\) 일 때 \[\begin{aligned} \left| f(x) - f(y) \right| &\leq M_{j_0}^n - m_{j_0}^n = M_{j_0}^n - U(x) + U(x) - L(x) + L(x) - m_{j_0}^n \\&\leq U(x) - L(x) + \epsilon\end{aligned}\] 가 됨을 알 수 있다.

위 부등식에 의해 \(y \in \{x : U(x) = L(x)\} \setminus\bigcup_{k=1}^{\infty} P_k\) 이면 \(f\)가 \(y\)에서 연속임을 알 수 있게 된다.

따라서, \(f\)가 연속인 점들의 집합을 \(C_f\)라 하면 \[\{x : U(x) = L(x)\} \setminus\bigcup_{k=1}^{\infty} P_k \subseteq C_f \subseteq\{x : U(x) = L(x)\}\] 이 된다. 한편 \(\bigcup_{k=1}^{\infty} P_k\)는 measure가 0 이므로, \(U = L\) \(m\)-a.e. 인 것과 \(f\)가 연속 \(m\)-a.e. 인 것은 동치이다. 위 논의의 결과를 이용하면 \(f \in \mathcal{R}[a, b]\) 인 것과 \(f\)가 연속 \(m\)-a.e. 인 것은 동치이다.

아래는 증명의 부산물입니다.

참고.

1. \(x \notin \bigcup_{k=1}^\infty P_k\) 이면 \(f\)가 \(x\)에서 연속 \(\iff f(x) = U(x) = L(x)\) 이다.
2. \(L(x) \leq f(x) \leq U(x)\) 이고 measurable function의 극한인 \(L(x), U(x)\) 또한 measurable이다.
3. \(f\)가 유계라는 조건이 있기 때문에 \(f \geq 0\) 인 경우만 생각해도 충분하다. \(\left| f \right| \leq M\) 라고 하면 \(f\) 대신 \(f + M\) 을 생각하면 되기 때문이다.

이제 리만 적분의 유용한 성질들을 가지고 와서 사용할 수 있습니다.

1. \(f \geq 0\) 이고 measurable일 때, \(f_n = f\chi_{[0, n]}\)으로 정의한다. 단조 수렴 정리에 의해 \[\int_0^\infty f \,d{x} = \lim_{n \rightarrow\infty} \int_0^\infty f_n \,d{x} = \lim_{n \rightarrow\infty} \int_0^n f \,d{x}\] 이다. 마지막 적분을 리만 적분으로 계산할 수 있다.
2. 닫힌 유계 구간 \(I \subseteq(0, \infty)\) 에 대하여 \(f \in \mathcal{R}(I)\) 라 하면 \(f \in \mathcal{L}^{1}(I)\) 이다. \(f_n = f\chi_{[0, n]}\) 으로 잡으면 \(\left| f_n \right| \leq f\) 이므로 지배 수렴 정리를 적용하여 \[\int_0^\infty f \,d{x} = \lim_{n \rightarrow\infty} \int_0^\infty f_n \,d{x} = \lim_{n \rightarrow\infty} \int_0^n f \,d{x} = \lim_{n \rightarrow\infty} \mathcal{R} \int_0^n f \,d{x}\] 임을 알 수 있다.
3. 마찬가지로 \(f_n = f\chi_{(1/n, 1)}\) 으로 잡은 경우에도 지배 수렴 정리에 의해 \[\int_0^1 f\,d{x} = \lim_{n \rightarrow\infty} \int_{0}^1 f_n \,d{x} = \lim_{n \rightarrow\infty}\int_{1/n}^1 f \,d{x} = \lim_{n \rightarrow\infty} \mathcal{R}\int_{1/n}^1 f \,d{x}\] 이 된다.